You are here: Start » Function Reference » Data Classification » Support Vector Machines » SVM_Init
SVM_Init
| Header: | AVL.h |
|---|---|
| Namespace: | avl |
| Module: | FoundationPro |
Initializes an SVM model.
Syntax
void avl::SVM_Init ( atl::Optional<float> inKernelGamma, float inKernelGammaScale, float inRegularizationConstant, atl::Optional<float> inNu, float inStoppingEpsilon, bool inUseShrinkingHeuristics, avl::SvmModel& outSvmModel )
Parameters
| Name | Type | Range | Default | Description | |
|---|---|---|---|---|---|
 |
inKernelGamma | Optional<float> | 0.0001 - 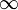 |
0.0001f | Gamma parameter for Rbf kernel |
 |
inKernelGammaScale | float | 0.0001 - 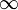 |
1.0f | Gamma parameter scale |
 |
inRegularizationConstant | float | 0.0001 - 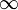 |
1.0f | Preventing overfitting |
 |
inNu | Optional<float> | 0.0001 - 1.0 | NIL | Tradeoff between training accuracy and number of SV |
 |
inStoppingEpsilon | float | 0.0001 - 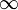 |
0.001f | Epsilon for stopping criterium |
 |
inUseShrinkingHeuristics | bool | True | May speed up computations | |
 |
outSvmModel | SvmModel& | Output model |
Description
The operation initializes a model for an SVM classifier that will be used by SVM_Train and SVM_ClassifySingle.
Support Vector Machines (SVM or C-SVC) is a classifier based on the support vector idea. Those vectors define hypersurfaces that separate data points from two different classes. The shape of those hypersurfaces is defined by the scalar product dependent on the kernel type. In the simplest case of linear kernel, they define hyperplanes.
Notice that SVM uses one-versus-all evaluation, because it is a binary classifier.
Nu-SVC is a variant of C-SVC making use of Nu parameter. It provides a tradeoff between the number of support vectors and the number of training errors. In fact, it defines a lower bound on the former and an upper bound on the latter.
There are two types of kernels:
-
Linear is a simple kernel for easier tasks. It is also recommended when the training time is critical.
The corresponding scalar product is \( L(u,v) = u^T v \). This kernel is used when inKernelGamma is equal to Auto. - Rbf (radial basis kernel) is the most common and the recommended kernel. Its function is \( \mathrm{Rbf}_{\gamma}(u,v) = \mathrm{exp}(-\gamma \|u-v\|^2) \).
SVM_Init parameters are:
- inKernelGamma is the \( \gamma \) (gamma) parameter for Rbf kernel. When it is set to Auto, then Linear kernel is used.
- inKernelGammaScale is used to provide more precise setting the value of inKernelGamma.
As the result kernel gamma value is set to \( \gamma = \frac{inKernelGamma}{inKernelGammaScale} \) - inRegularizationConstant is the C constant of C-SVC and Nu-SVC. With greater C, the model is less likely to overfit training data.
- inStoppingEpsilon defines precision of the training. The smaller this parameter is, the more accurate the training is, but also the longer it takes.
- inNu is the Nu parameter of Nu-SVC described above. If it is Auto, then simple C-SVC classifier is used.
- If inUseShrinkingHeuristics is set, the algorithm will use the heuristics that shrinks the search region to speed up computation with little or none loss of accuracy.
Getting started:
At the beginning a good choice for SVM type is C-SVC (i.e. to leave inNu equal NIL) and the recommended kernel type is Rbf. The parameter inStoppingEpsilon may be left default (equal 0.001) and it is recommended to set inUseShrinkingHeuristics to true. There are two parameters to choose: inKernelGamma and inRegularizationConstant. The first one is responsible for "tightness" of the class regions and the second one for ignoring detached data points.
The best way to choose those parameters is to perform a grid search, i.e. to try different pairs of values, for example pairs of powers of 2. The grid search may be performed on a relatively small subset of training data to reduce training time. Moreover, it is recommended to use cross-validation, which means evaluating parameters not on the training data, but on a different data set, to prevent overfitting. One has to remember to choose those subsets at random.
Another thing worth trying is normalizing data before passing it to training and classification procedures. However, data has to be rescaled with the same value for both training and classification data! Normalizing data might improve performance and is useful for optimal parameter choice. If the data vectors are rescaled \( N \) times, then gamma in RBF kernel has to be rescaled by term \( N^{-2} \) to ensure similar performance.
Remarks
See Also
- SVM_ClassifySingle – Classifies input features based on a trained model.
- SVM_Train – Trains an SVM model.

