Back to Aurora Vision Studio website
You are here: Start » Filter Reference » Geometry 2D » Geometry 2D Spatial Transforms » SplitSegment
| Module: | FoundationLite |
|---|
Splits a segment into several parts of equal length.
| Name | Type | Range | Description | |
|---|---|---|---|---|
 |
inSegment | Segment2D | ||
 |
inCount | Integer | 1 -  |
Number of segments after segment split |
 |
outSegments | Segment2DArray | ||
Description
Filter computes outSegments using following formulas:
$$\mathbf {outSegments}[0].x_{begin} = \mathbf {inSegment}.x_{begin}$$
$$\mathbf {outSegments}[0].y_{begin} = \mathbf {inSegment}.y_{begin}$$
$$\mathbf {outSegments}[0].x_{end} = \mathbf {inSegment}.x_{begin} + \Delta x$$
$$\mathbf {outSegments}[0].y_{end} = \mathbf {inSegment}.y_{begin} + \Delta y$$
$$\mathbf {outSegments}[i].x_{begin} = \mathbf{outSegments}[i-1].x_{begin} + \Delta x $$
$$\mathbf {outSegments}[i].y_{begin} = \mathbf{outSegments}[i-1].y_{begin} + \Delta y $$
$$\mathbf {outSegments}[i].x_{end} = \mathbf{outSegments}[i-1].x_{end} + \Delta x $$
$$\mathbf {outSegments}[i].y_{end} = \mathbf{outSegments}[i-1].y_{end} + \Delta y $$
$$ i = 1, 2, .., \mathbf {inCount} - 1 $$
where
$$\Delta x = \frac {\mathbf{inSegment}.x_{end} - \mathbf{inSegment}.x_{begin} }{\mathbf{inCount} }$$
$$\Delta y = \frac {\mathbf{inSegment}.y_{end} - \mathbf{inSegment}.y_{begin} }{\mathbf{inCount} }$$
Examples
Assume segment described with two points:
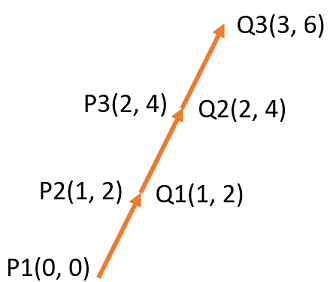
Result will be as follows:
$$\mathbf {outSegments}[0]=\vec{P_1Q_1}=[1, 2] \quad \mathbf {outSegments}[1]=\vec{P_2Q_2}=[1, 2] \quad \mathbf {outSegments}[2]=\vec{P_3Q_3}=[1, 2]$$
- Start point P(0, 0)
- End point Q(3, 6).
Result will be as follows:
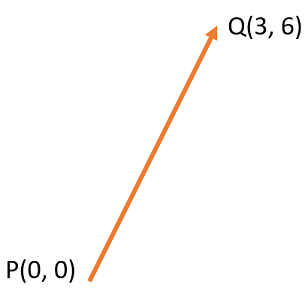 |
 |
Complexity Level
This filter is available on Basic Complexity Level.

 Basic
Basic